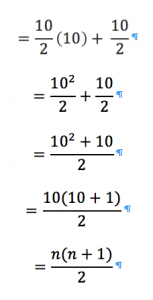Fall 2009, I started my IB Diploma, first year chemistry class with Mastermind, the logic board game. One of the objectives, detailed in the Teach, To learn; Learn, to Teach blog post, was to give my students a taste for scientific modelling and deductive reasoning. In other words, to give them a taste for how science works and how scientists work.
In this blog post, I shall describe, in greater detail, what I did in the Mastermind lessons.
Mastermind
A codemaker secretly places 4 large pegs of any color behind the shield (see image at the top) and the opponent (the codebreaker) attempts to break the code by guessing and placing the large pegs on the rows of holes on the tray.
After every guess, the codemaker indicates on the side whether any of the colors are correct but not their position (small white peg) and/or if any of the colored pegs are in the correct position (small red peg). Using those information then the codebreaker proceeds to crack the code by deduction.
With my students, I randomly created a code in full view of the students and then worked through a series of guesses explaining my reasoning — how I made my deductions.
Then I gave them a code to break. Following that, I had them create codes for one another to break in turn. I then followed that up with the challenge, the challenge to analyze the game for all the possible codes.
There are a number of ways of approaching the challenge. One is through modelling.
Scientific modelling, among other things, is a way of thinking that scientists use to arrive at precise mathematical equation or a set of description for a process — or phenomenon — that defies description through direct observation, or measurement, etc. Therefore, it’s important to expose science students — future scientists — to it.
Here, modelling involves starting with the simplest combinations and then working up, by changing one variable at a time, until we get the solution to the combination in question.
Incidentally, in the analysis below, I have used the method of determining the probability of what is called independent events in Probability and Statistics.
Let’s start by looking at what happens to the number of UNIQUE codes possible codes (challenge #1) when keeping one of the two variables constant and changing the other.
A. The simplest combination:
# of holes = 1,
# of different color pegs = 1.
Then the number of codes = 1.
Next, since it’s easier to increase the number of different color pegs, let’s do that.
# of holes = 1,
# of different color pegs = 2.
Then, number of codes = 2.
Three different color pegs, number of codes = 3.
In other words, the number of codes = number different color pegs.
To conclude then, when # of holes is 1, number of possible codes equals the number of different-color pegs.
Simple enough!
B. Now let’s go back to the beginning and change the number of holes but keep the number of different color pegs:
# of holes = 2,
# of different color pegs = 1.
Then number of codes = 1.
Increasing the number of holes does NOT change the number of codes. The number of codes will always be = 1.
To conclude then, as long as the number of different color pegs is 1, the number of codes that can be generated remains 1 regardless of the number of holes.
That wasn’t so hard, was it?! 😉
Let’s move on…and look at what happens to the number of possible codes for other combinations.
C. Keeping # of holes constant (to 2) but changing the number of different color pegs.
| 1. Number of different color pegs = 1 Number of UNIQUE codes (ignoring position) = 1 |
Red RR |
| 2. Number of different color pegs = 2 Number of codes (ignoring position) = 3 |
Red (R) and Green (G). RR, RG (or GR), GG. |
| 3. Number of different color pegs = 3 Number of codes = 6 |
Red (R), Green (G), Yellow(Y). RR, RG, RY, GG, GY, YY . |
| 4. Number of different color pegs = 4 Number of codes = 10 |
Red (R), Green (G), Yellow(Y), Black(B). RR, RG, RY, RB, GG, GY, GB, YY, YB, BB. |
What patterns do you see? You should see at least two!
Let me give you a hint about one of them. (We’ll look at the other pattern in the next stage.) Look at the color combinations!
| For 2 colors, the codes are 2 for the first color and then 1 for the second, (or 2 codes of single-color pegs and 1 of two-color pegs) | i.e. 2 + 1 = 3. |
| For 3, 3 for the first, 2 for second and 1 for the last (or 3 codes of single-color pegs and 3 of two-color pegs) | i.e. 3 + 2 + 1 = 6 |
| For 4 it’s 4 for the first color, then 3, then 2 and then 1 for the last (or 4 codes of single-color pegs and 6 of two-color pegs) | 4+3+2+1 = 10. |
| In other words, for n different color pegs, the number of codes possible = | n + (n – 1) + (n – 2) + …..+ 3 + 2 + 1 |
| Or, looked at another way, the number of codes possible = | 1 + 2 + 3 + …. + (n – 2) + (n – 1) + n |
Which is just the sum of the natural number from 1 all the way to n. (What pattern do you see in the breakdown of the codes within the brackets?)
Is it possible to deduce a considerably more compact formula? What happens when n, for instance, is equal to 10?
| Number of possible codes
Rearranging Restating the values in term of 10
Simplifying and substituting n for 10 |
= 1 + 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10
= 1 + 9 + 2 + 8 + 3 + 7 + 4 + 6 + 10 + 5 = 10 + 10 + 10 + 10 + 10 + 10/2
|
So, when number of holes equals 2, for n different color pegs, number of possible codes equals [n(n + 1)]/2!
You could test the validity of the formula by comparing the number of codes for when the number of colored pegs is equal to 5!
D. # of holes = 3. (Incidentally, codes in red represent the new codes from the preceding.)
| 1. Number of different color pegs = 1 Number of codes (ignoring position) = 1 |
Red RRR |
1 |
| Code variety: | 1 (of one color variety) | =1 |
| 1. Number of different color pegs = 2 Number of codes (again ignoring position) = 4 |
Red (R) and Green (G)). RRR, RRG (or RGR or GRR), RGG (or GRG or GGR), GGG |
3 1 |
| Number of codes of each variety: | 2 (of one color variety) + 2 (of 2 of one and 1 of other color variety) | =4 |
| 2. Number of different color pegs = 3 Number of codes = 10 |
Let’s say again Red (R), Green (G), Yellow(Y)). RRR, RRG, RGG, RRY, RYY, RGY, GGG, GGY, GYY, YYY |
6 3 1 |
| Number of codes of each variety: | 3 (of 1 color) + 6 (of 2 colors) + 1 (of 3 different colors) | =10 |
| 3. Number of different color pegs = 4 Number of codes = 20 |
Red (R), Green (G), Yellow(Y), Black(B)). RRR, RRG, RGG, RRY, RYY, RGY, RRB, RBB, RGB, RYB, GGG, GGY, GYY, GGB, GBB, GYB YYY, YYB, YBB, BBB, |
10 6 3 1 |
| Number of codes of each variety: | 4 + 12 + 4 | =20 |
| 4. Number of different color pegs = 5 Number of codes = 35 |
Red (R), Green (G), Yellow(Y), Black(B), Purple(P)). RRR, RRG, RGG, RRY, RYY, RGY, RRB, RBB, RGB, RYB, RRP, RPP, RGP, RYP, RBP GGG, GGY, GYY, GGB, GBB, GYB GGP, GPP, GYP, GBP YYY, YYB, YBB, YYP, YPP, YBP BBB, BBP, BPP, PPP |
15 10 6 3 1 |
| Number of codes of each variety: | 5 + 20 + 10 | =35 |
Again, do you see any pattern? You should have noted at least two.
The one in the final column is quite easy to see! The other, in the numbers breaking down the codes by type of codes (single-, two- or three-color codes), is just a little more difficult but not impossible to decipher.
Let’s have a closer look at the final column of numbers.
| For 1 color, the number of codes = 1 | (# of codes) = # of colors, which is equal to 1. |
| For 2 colors, the number of codes = 4 | # of codes for 1 color (1) + increment (3) i.e. 1 + 3 = 4 |
| For 3 colors, the number of codes = 10 | # of codes for 2 colors (4) + increment (6) Substituting, [# of codes for 1 color (1) + increment (3)] + increment (6) i.e. 1 + 3 + 6 = 10 |
| For 4 colors, the number of codes = 20 | # of codes for 3 colors (10) + increment (10) Substituting, [# of codes for 2 colors (4) + increment (6)] + increment (10) Substituting again, [{# of codes for 1 colors (1) + increment (3)} + increment (6)] + increment (10) i.e. 1 + 3 + 6 +10 = 20 |
| For 5 colors, the number of codes = 35 | # of codes for 4 colors (20) + increment (15) Substituting, [# of codes for 3 colors (10) + increment (10)] + increment (15) Substituting again, [{# of codes for 2 colors (4) + increment (6)} + increment (10)] + increment (15) Substituting again, [{(# of codes for 1 colors (1) + increment (3)) + increment (6)} + increment (10)] + increment (15) i.e. 1 + 3 + 6 + 10 + 15 = 35 |
What do you notice about the difference in the increment each time the number of colors of pegs is increased by one? It’s equal to the number of different color pegs in the latter!
In other words, total number of codes possible for when 5 colored pegs is used as opposed to 4, the difference in the increments going from 3 to 4 (10) and 4 to 5 (15) must be 5, which it is (15 – 10 = 5). Knowing that, we can easily predict the number of codes for when 8 different colored pegs are available.
Starting with the number of codes for when only a single color peg is used, here’s what the increments for when an additional different colored peg is introduced will look like (for 8 different colored pegs): 1, 3, 6, 10, 15, 21, 28, 36. To determine the number of codes, all you now have to do is add them up, which comes out to 120.
What about the pattern in the variety of codes the different number of color pegs produce? For each variety — single-color, two-color and three-color — there is a pattern in their values and/or their increment.
For instance, the number of single-color codes — first number in the second column of code variety row — is equal to the number of different colored pegs.
The two-color variety — first number in the second colume of code variety row — increases by (n – 1) x 2 where n = the number of different color pegs and must be equal to or greater than 3.
As for codes consisting of three different colored pegs — the third number in the second column of code variety row — the difference in the increment increases by 1. Increment in going from 1 (0) to 2 (0) is 0. Increment in going from 2 (0) to 3 (1) is 1. So therefore, the difference in the two increments (1 – 0) is equal to 1.
Now, in going from 3 (1) to 4 (4) the increment is 3. Comparing the increments going from 2 to 3 and 3 to 4, the difference is (3 – 1) 2.
There you have it!
Now, all that’s left is to figure out the number of codes possible when the number of holes is 4 and the number of different color pegs is 8. Go ahead and try it!
I can’t have all the fun; I have to leave some fun for you too! 😀
And what about challenge number 2?
Well, all you need to do is to actually count what was ignored in the above process and then figure out the pattern! 🙂
A Note For Teachers
If you decide to use Mastermind in your class, you could start with what I did. Here are images of two codes that have already been broken.
 |
 |
You could start the discussion by getting your student to talk about why I have begun to crack both the codes in the same way — trying out all eight colors in the first two guesses. Then discuss what the hints indicate about the code. Next, justify logically the next two guesses which are different even though the codes are similar…and so on until the last guess.
It’s important to point out that there isn’t necessarily a single “right” guess at each stage until of course the last one! Just that some guesses might end up taking longer to crack the code than others.
If you were to have your students perform the kind of analysis I have done — figuring out the number of possible codes — there are of course other ways of analyzing it. You might want to stress that!
And finally, those who are mathematically minded, don’t need to go through this reductive exercise! I am sure they can quite easily figure out the formula using probability theories for instance!
Mastermind and Science
The game of mastermind, required the use of information to make logical deductions about the code. Science also involves using information/data to logically arrive at explanations for a host of scientific phenomenon.
What specific relationship does this analysis have to Chemistry? Just as the above analysis, Chemistry is also about patterns. The Periodic Table, for instance, is a table of patterns in the properties and behavior of chemical elements! As a matter of fact, you can say that Science in general is a study of patterns!
What’s more, how we went about figuring out what happens to the number of possible codes with changes in the number of different color pegs and holes is similar to how we would perform experiments involving the study of the effect of different variables on the results of an experiment. We generally keep everything constant and change/vary only one of the variables at a time.
As for the reductive approach to figuring out mathematical equations for the possible number of codes…. Mathematical equations that describe a process or event or a system or their general characteristic etc. is quite common in Science. For instance, the Kinetic Theory of Gas, which is the basis for the Ideal Gas Equation is derived by a similar process of reductive modelling. In quantum mechanics, the behaviour and characteristics of quantum particles is determined by, and I am not making this up, “the particle in the box model“!
So you want to have a go at the challenges? Go ahead! Have a go below in the comment section! And good luck!