The first two paragraphs in this brilliant piece by two tenth graders reminded me of how math education in Nepal had failed me and fails our students in Nepal.
Another thing the article reveals — though nothing new — is how our children are totally aware of how poor and screwed up our education system is. I too was aware of that as a student. Luckily for me, our North-American teachers — of whom my class had a number of from grade 5 onward — salvaged my education and were my inspiration. The awareness raised by and inspiration from those teachers were partly the drive behind my dream of going to the US for further studies. I made it but via Italy.
At the United World College of the Adriatic, in my favorite pizza country, I discovered — among a host of other things — how poor my math education had been ! 🙂
But before that…let me get back to the article. Starting with a simple mathematical problem, the article very clearly outlines a number of major issues Nepali Education System suffers from and how it thus fails a vast majority of our students. The problem (see image below) is about the number of handshakes a group of people make, which the writers were able to solve.
They solved it by using a formula they had committed to memory. To demonstrate what’s wrong with our education system, the young writer-duo go on to describe how they couldn’t explain how or why the formula worked. Of course, I am NOT surprised at all that the two struggled to do that!
In my workshops for teachers, when I have challenged them with similar problems, a majority struggled to tackle them, AND those who were able by resorting to formula, most couldn’t explain it either.
Many teachers couldn’t even BEGIN to analyse or process information and think — and work — through a problem by applying concepts and their understanding to arrive at a solution! Forget about teaching it to students, of course!
Besides, in our education system, whether a student is able to magically come up with the answer applying a formula or by recall is of more importance and value than anything else. THINKING — analyzing, applying, evaluating, and synthesizing — is valued little to none by the system (neither is being DIFFERENT). So, why teach or care to teach how to think through a problem and tackle it?!
No surprise then that students can’t display higher level thinking skills either.
No wonder I struggled with math in Italy, a different education system, doing International Baccalaureate higher level math.
And you want to know what the crazy thing about me and math was? I was one of the top students in my class in the subject (and in general). My highest scores throughout school had consistently been in the subject.
I discovered that all I had been taught and was good at was memorizing formulae, the order of steps and rules for solving mathematical problems, and regurgitating them to solve problems already solved in the past. I had never really been taught, and therefore learned, how a formula worked, where they came from, why they worked, and what or how — or if — they in anyway reflected something in or about life and the real world. More than thirty years later, students like the write-duo appear to NOT be taught any of that either.
If we had been taught HOW a formula is arrived at — i.e. the logic behind it — through MODELLING, for example, we would have learned HOW to think. (Modelling, incidentally, is something we do a lot of in Science, as well as in mathematics.) Then, we would have been able to explain WHY the formula worked.
More importantly, we would have been in a position to even DERIVE formulae for novel problems not attempted in class, then arrive at A solution to them, whether right or wrong. The answer or solution, incidentally, would have been besides the point, especially if the problem had been an open-ended variety. The process, when carried through again and again, would have given us an insight into the way the great THINKING mathematicians and scientists discovered or derived the numerous formulae we use and accept as valid.
In the Nepali education system, however, answers are given undue importance, especially an answer that’s been deemed to be CORRECT, even when they are disputable. Real life problems, however, don’t necessarily always have THE correct answer or solution.
So, naturally, the question you are probably asking is, what if a teacher were interested in imparting those skills to students using the above problem of handshakes?
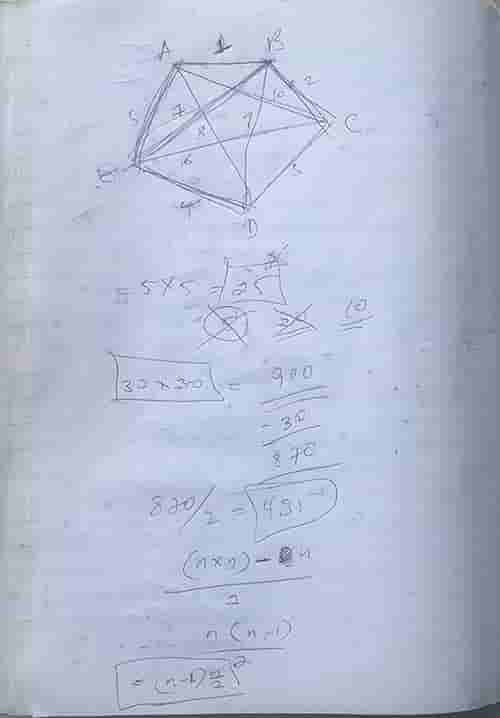
How could a teacher have modeled the problem to arrive at the “multiplying the total number of people by the number one less than itself, and dividing the outcome by 2” formula? A student of mine and I tackled just that a few days ago but changing the problem slightly to one of 30 guests attending a party.
The first instinct, the knee-jerk tendency is to just multiply the number of guests by itself, which is wrong. What is wrong with it is revealed by modeling.
There’s at least two ways of modeling the problem.
One is by sequentially figuring out the number of handshakes starting with “0” guests, which is easy to do AND does NOT require advanced mathematical skills.
After figuring that out for for several different number of guests, a formula can be arrived at by STUDYING/ANALYZING the pattern. That, again, does NOT require advanced mathematical skills! Most people are able to pick out at least a few different patterns in the numbers one gets EVERY SINGLE ONE OF WHICH can be used to arrive at the formula! I haven’t done the last part myself but I am pretty sure of it.
Anyway, when doing this, my young 8th grade student had the brilliant idea of visualizing the handshakes using geometric shapes and lines between the corners to represent them! He drew a pentagon for when the number of guests is 5, for example, like the one in the image below (which, incidentally, is my working). (I make notes when I am teaching students online! And that, incidentally, is one of the many MANY instances of a student teaching me something new.)
As you can see above, we were able to derive the formulae, the same formulae the twins recalled and used to solve the problem. I’ll leave it up to you to figure out the logic behind it all. 🙂
The other way of modeling the problem is by imagining the guests arriving at different times AND one at a time. That way you can quite easily determine the number of handshakes by a guest by order of arrival at the party. Can you do that?
I doubt my memory is failing me but, to reiterate, I don’t EVER remember performing an analysis of the kind above in my math classes in Nepal. No wonder I struggled with math in a different education system, one where I was required to THINK and reason.
To conclude, analyzing and processing information and putting them together to arrive at a solution to a problem — problem solving — is a crucial everyday skill, more important than being able to recall the right answer. That, however, is something Nepali education system does NOT value, and therefore, does NOT teach.
In teaching our children to NOT think, by my estimate, our education system in Nepal fails 90% of students. In order for it to actually serve a majority of the students, the system must be completely overhauled.
What do you think?
(If you are interested in learning more about Modeling and you would like a bit more challenging problem — to do with figuring out the number of codes in the board game of Master Mind — have a look at Modelling…Without The Catwalk, a blog post in my Science Blog. If you are interested in another mathematical challenge problem and kind of topical one in these times of the coronavirus pandemic, check out Card Problem, Exponential Growth, and COVID19.)